วิธีสร้างและแก้ปริศนาลอจิก

ปริศนาลอจิก มาในรสชาติที่แตกต่างกันสองสามแบบ ที่พบบ่อยที่สุดคือปริศนาตารางตรรกะ ปริศนาความรุนแรงเชิงพื้นที่ และปริศนาการคิดด้านข้าง

ปริศนาตารางลอจิก (ซึ่งรวมถึง ปริศนาซูโดกุ และปริศนา KenKen) ส่วนใหญ่จะพบเป็นปริศนาประเภท "ใครเป็นเจ้าของม้าลาย" ความท้าทายของปริศนายอดนิยมเหล่านี้คือการสืบหาข้อเท็จจริงบางอย่างและบรรลุข้อสรุปโดยใช้เหตุผลแบบนิรนัยเพื่อประมวลผลข้อความหลายคำ

ปริศนาการหักเงินเหล่านี้เป็นปริศนาตรรกะพื้นฐานที่สุดและสามารถสร้างได้อย่างง่ายดายด้วยระดับความซับซ้อนที่แตกต่างกันเพื่อดึงดูดทุกระดับ ความสามารถในการแก้. โดยความแตกต่างของจำนวนองค์ประกอบ ปริมาณของข้อมูลที่ให้ตลอดจนการเชื่อมต่อระหว่างกันของ ข้อความที่กำหนด (เช่น การเชื่อมโยงโดยตรง/หลวม) ปริศนาเหล่านี้อาจเป็นเรื่องง่ายเหมือนวงกลมหรือยากเหมือน เล็บ.

ตัวอย่าง: A Day at the Races

ในฐานะพนักงาน แจ็คมาถึงสนามแข่งเพื่อค้นหานักขี่ม้าสามคนคือวิลลี่ เอ็ดดี้ และฟิเดล นั่งอยู่ในห้องสื่อเพื่อรอการแถลงข่าวเริ่มต้น เจ้านายของแจ็ค (ผู้ชื่นชอบปริศนา) ได้ทิ้งโน้ตไว้เพื่อแนะนำให้เขานำผ้าไหมสำหรับนักแข่งแต่ละคนมาให้เขา และประกาศให้สื่อมวลชนทราบว่านักแข่งแต่ละคนชนะการแข่งขันใดและม้าตัวใดที่เขาขี่ม้าอยู่

ความท้าทายสำหรับแจ็คคือบันทึกของเจ้านายของเขามีเพียงหกข้อความ:

1. วิลลี่ไม่เคยชนะเคนตักกี้ดาร์บี้
2. นักขี่ม้าที่ขี่ Flash ไม่ได้สวมผ้าไหมสีน้ำเงิน
3. ผู้ชนะของ Belmont Stakes ไม่ได้ขี่ Zipper
4. ผู้ชนะ Preakness จะอยู่ทางขวาของ Willie
5. จ็อกกี้ที่ขี่ Flash นั่งอยู่ทางด้านซ้ายของผู้ชนะดาร์บี้
6. นักขี่ม้าที่ขี่ Zipper นั่งอยู่ทางด้านซ้ายของนักขี่ม้าที่สวมชุดสีเหลือง

เป็นไปได้ไหมที่แจ็คจะรู้ว่านักจัดรายการคนใดสวมผ้าไหม เขาชนะการแข่งขัน และขี่ม้าตัวใดโดยใช้เหตุผลแบบนิรนัย

สร้างตารางลอจิก

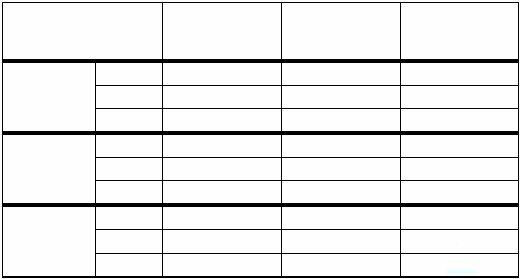
ในการเริ่มต้น แจ็ควาดตารางที่มีสี่คอลัมน์และสี่แถว จากนั้นแบ่งย่อยสามแถวล่างออกเป็นสามแถวตามที่แสดงไว้ด้านบน (รูปที่ 1)

ในแถวบนสุด เขาเขียนชื่อจ๊อกกี้ตามลำดับ (วิลลี่, เอ็ดดี้, ฟิเดล) และใส่ตัวแปรทั้งเก้าไว้ในคอลัมน์ด้านซ้ายมือ

จากนั้นเขาก็เขียนข้อความทั้งหกด้านล่างตาราง

บันทึก: ข้อความที่อ้างถึงด้านซ้ายและขวามาจากมุมมองของผู้ชมเมื่อดูจ๊อกกี้ในงานแถลงข่าว (ในตาราง)

ตอนนี้แจ็คอ่านแต่ละข้อความเพื่อดูว่าเขาสามารถหาข้อสรุปใดสำหรับแต่ละข้อได้

• วิลลี่ไม่เคยชนะ เคนตักกี้ดาร์บี้.

นี่เป็นคำแถลงที่ตรงไปตรงมาและอนุญาตให้แจ็คกำจัดตัวเลือกการแข่งขันเพียงตัวเลือกเดียวสำหรับวิลลี่

• นักขี่ม้าที่ขี่ Flash ไม่ได้สวมผ้าไหมสีน้ำเงิน

คำพูดนี้ไม่ได้ช่วยอะไรจนกว่าแจ็คจะรู้ว่าใครขี่แฟลชหรือใครสวมชุดสีน้ำเงิน เขาวางสิ่งนี้ไว้สำหรับตอนนี้

• ผู้ชนะของ Belmont Stakes ไม่ได้ขี่ Zipper

เป็นอีกครั้งที่แจ็คจำเป็นต้องรู้ว่าใครชนะเบลมอนต์หรือขี่ซิปก่อนเขาจะสรุปอะไรจากคำกล่าวนี้

• ผู้ชนะ Preakness จะอยู่ทางขวาของ Willie

ตอนนี้แจ็คสามารถก้าวหน้าได้แล้ว ก่อนหน้านี้เขากำจัดดาร์บี้เป็นตัวเลือกสำหรับวิลลี่ และตอนนี้เขาสามารถกำจัดพรีกเนสได้ ซึ่งหมายความว่าเขาสามารถสรุปผลในตอนแรกได้ วิลลี่ชนะเดิมพันเบลมอนต์ ธาดา! นอกจากนี้ เขายังสามารถกำจัดซิปเป็นตัวเลือกสำหรับวิลลี่ (ดูข้อความ #3)

• จ็อกกี้ที่ขี่ Flash นั่งอยู่ทางด้านซ้ายของผู้ชนะดาร์บี้

จากคำกล่าวนี้ Jack กำจัด Flash ให้เป็นตัวเลือกสำหรับ Fidel เนื่องจากเขานั่งอยู่ทางขวาสุด ตอนนี้เขารู้แล้วว่าวิลลี่หรือเอ็ดดี้ขี่แฟลช

• นักขี่ม้าที่ขี่ Zipper นั่งอยู่ทางด้านซ้ายของนักขี่ม้าที่สวมชุดสีเหลือง

คำพูดนี้ทำให้แจ็คสรุปได้ว่าเอ็ดดี้ขี่ซิปเพราะผู้จัดรายการเพียงคนเดียวที่อยู่ทางซ้ายของใครก็ตามคือวิลลี่ซึ่งแจ็คสรุปไว้ก่อนหน้านี้ไม่ได้ขี่ซิป นอกจากนี้ ฟิเดลต้องสวมชุดสีเหลือง และวิลลี่ต้องขี่แฟลช

ตอนนี้แจ็คกลับมาที่คำสั่ง #2 จากคำกล่าวนี้ เขาสรุปได้ว่าวิลลี่ต้องใส่สีแดง ซึ่งหมายความว่าเอ็ดดี้ต้องใส่สีน้ำเงิน

และนั่นก็ทำให้ปริศนาสมบูรณ์ เยี่ยมไปเลยแจ็ค!

วิธีสร้างปริศนาลอจิก

1. วาดตาราง

   วาดเส้นตารางอย่างง่าย ใช้อันข้างต้นเป็นแนวทาง

2. สร้างสถานการณ์

   ชาวประมงสามคน (ปลา เทคนิค สถานที่) นักดนตรีสามคน (เครื่องดนตรี เพลง แนวเพลง) สามคนในบาร์ (อาชีพ ดื่ม ของว่าง) เป็นต้น

3. กำหนดค่าต่างๆ

   หลังจากที่คุณดินสอในส่วนหัวแล้ว ให้กำหนดค่าที่แตกต่างกันสามค่าให้กับอักขระทั้งสามตัวแต่ละตัว

4. ทำงานย้อนหลัง

   เมื่อคุณกรอกตารางแล้ว ให้ทำงานย้อนกลับและสร้างคำสั่งที่จะช่วยให้ผู้แก้ปัญหาสามารถอนุมานค่าสำหรับอักขระแต่ละตัวได้

   เช่นเดียวกับการระบุคุณค่าของตัวละคร ผสมในข้อความที่บอกว่าตัวละครไม่มี/ทำ ("ผู้เล่นแซ็กโซโฟนไม่เขียน เพลงบัลลาด") และ/หรือที่อ้างถึงความสัมพันธ์ของค่านิยมและไม่ได้อ้างอิงถึงตัวละครโดยตรง (ผู้เล่น R&B ร้องเพลงแจ๊ส คลาสสิก) พยายามจำกัดตัวเองให้อยู่แค่ห้าหรือหกประโยค

5. ทดสอบแก้

   ทดสอบแก้ปริศนาเพื่อให้แน่ใจว่าใช้งานได้ ตรวจสอบให้แน่ใจว่าคุณไม่มีเบาะแสที่ไม่จำเป็นหรือซ้ำซาก กล่าวอีกนัยหนึ่ง เบาะแสหรือข้อความสองคำที่นำไปสู่ข้อสรุปเดียวกัน

   เป็นความคิดที่ดีที่จะมีคนทดสอบ ไขปริศนาของคุณ เพื่อความถูกต้องและเป็นธรรม